Good fried rice.
This post is a linear progression through todays’ Interactive Web Publishing class. This post is for everyone, and thus why I’ve included it on my blog. For future students, this may provide an insight of what goes on in this class, and if they’d like to take part. For current students, it could reinforce what happened today, just in case they missed anything. And for the general public, we talked about some very interesting interactive concepts.
As a quick interduction, I’m taking a class at the Friends World College, East Asia Center, in Kyoto, Japan, called Interactive Web Publishing. This course explores how to create a personal learning community on the web using tools like blogs, bloglines, and interacting with others who are building their own learning communities, in order to learn, teach, and converse with many differing outlooks.
As I said, I’m going to take this post in a very time-wise linear progression, and this will be kind of journal like.
I actually arrived first, and early, so on the board I wrote the innocent quote: “The key to having good fried rice, is the ability to fry.” I just randomly made it up, and searching google leads me to believe I’m the originator.
Well, then the teacher came in, and we started off talking about some various concepts outside of class, including Graphene Computing, Rolled up Monitors, One handed keyboards, Aquariums in Osaka, and what Higher Mathematics (post calculus) seems to really be about. I then brought up something that would lead us to the rest of the lesson. However, Bryan came in, and we got momentarily sidetracked by creating surveys online, possibly using SurveyMonkey.com. We also discussed ethics of writing evaluations of other students’ blogs, and how to constructively critisize without insult. And then we got distracted by embedding video’s into blog posts, and came to the conclusion that a search of “embedding video blog” in Google will bring up some good sources.
Back to the topic. I had mentioned earlier one of my concerns about placement of goals. For example, an MMORPG that I tend to like is called Fly For Fun. In it, many people can interact online, and eventually when they reach level 20 (I believe the max is 99ish), they gain the ability to get either a broomstick or hoverboard, and thus able to fly. However, I notice many players play FlyFF for the sole purpose of flying, and thus they level to 20, fly around for a bit, and then quit the game. This always bothered me, because they tended to not enjoy the game, and not ever return to it. I felt that students may feel the same about this class, making a blog for the sake of passing the class, but not really doing anything constructive or interesting with it, because their goals are set too short.
This idea sparked something in Aaron, our teacher, which he was actually just thinking about this this morning as well. An idea about what is called the Personal Learning Ecology. This is another metaphor for the p2p concept of a read/write web, instead of a read only web. As in a nature based ecology, an ecology on the web is the interactions of a large number of bloggers who sometimes come together to share ideas and conversation, and then sometimes split apart and share things with other members of the ecology. The PLE is constantly in motion, and everyone learns something, as well as teaches. In this environment, the roles of Teacher-Apprentice are constantly switiching. As Aaron posted out, my blog about Hyperobjects is something he knows next to nothing about, and thus is taking on the role of the apprentice, while his blogs on teaching theory is something I know hardly anything about, and thus I become the apprentice. Unlike static school systems, where there are clear definitions and roles of all participants, a PLE would provide education through peer discussions, finding someone who knows more, and teaching those who know less. Aaron seems to be interested in education, and thus his blog post focuses on how this idea of an ecology could be applied to school systems that would overtake the old style of heirarchical education.
As Aaron said, they key is to synthesize, to take what is learned, and combine it together, and with other sources, and a personal opinion and offer it up to the rest of the ecology, who should then use that along with other sources and their own ideas to build upon the work offered. The same idea is what was bothering me about the game, players would take for themselves, and then leave without really interacting with the community. Similarly this occurs with bloglines, where subscribers read their feeds, but hardly ever combine the various posts into a single post, and present something new to the community.
This very idea lead Aaron in his creation of Week 10 assignments, in which we, the class, should do an experiment of combining multiple posts from bloglines, adding material from other sources, and using all of that in a blog post. Then to see if we can do that on a weekly basis.
Describing this, Aaron pointed out Steve’s blog. What happened was Steve made a podcast about Enka, and Aaron added it to the Friends World podcast site while including a picture he found from Flickr. From there, the photographer commented on the post, and Steve ended up following it up with another podcast that incorporated the photographer’s input.
Aaron also talked a bit about the final paper that will be due, how there are guidelines to writing it, but it can be about anything that the class wants to write about. I’ll probably be updating the “What is Blogging” page in the formation of this paper, so anyone interested in the purpose, and ways of blogging, keep that in mind.
We took a look at my quote that I randomly created, and noted how much it applied to todays lesson. That is, that the goal of doing something is more important than the goal of learning something. Learning how to blog, shouldn’t be the sole purpose. The creation of a Personal Learning Ecology is important, and learning how to blog is key to getting there.
2 Comments
Sequences through the Dimensions
Today I’d like to discuss two sequences that appear while traversing higher dimensions.
First I’d like to introduce everyone to two shape families. The first is most likely to be more familiar than the other one, and that is the square/cube/tesseract family. For the time being I’ll call them by their common names, then introduce my naming scheme, leading into the second family. From there I’ll contine to talk about the sequences that appear, and if possible, add proofs of the sequences.
Before moving on, I’d like to point out that the 0th dimension is a singularity, or a point. It has no measurable distance in any way. Meanwhile the 1st dimension is a line. It has only length, no width, no height. Kind of like a very thin string. 2nd dimension is a plane, it is kind of like the x-y graphs that you could play with shapes in in geometry class. 3rd dimension is basically what we live and orient in. We have height, width, and length. With those three values, you can pinpoint anything in this galaxy.
As I said, the first family we will discuss is the one that includes squares and cubes. As all of these Dimensional Shape Sequences, it starts with a Point in the 0th dimension. The goal of this particular sequence when incrementing dimensions is to ‘drag’ the object perpindicular from itself.
| In this first image, I demonstrate the first shape in the Sequence, that corrosponds to the 0th dimension. I have in the background a tesseract, because that’s our goal for this sequence. |
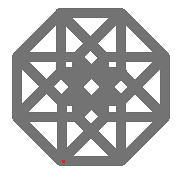 |
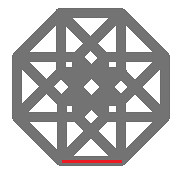 |
Following our ‘algorithm’ we take this point, and drag it for a unit distance perpendicular to itself. It turns out that we chose the perpendicular that ran across the bottom of the tesseract. Note how this new figure, the second in our sequence, now has two points, and one line. These points act as a ‘wall’ encompasing a small amount of the current dimension (in this case 1st dimension, this dimension extends infinitely in both directions.) Also, as we go along, pay attention to the lines connected to our first point. |
| To get to our next figure, we take our original figure, and drag it perpendicular to itself. This time we end up with a square. In this figure notice how the two points in the original, doubled, and created lines between the original points and their duplicates. Also, notice how the line from the original doubled itself, and within it created a plane. This is very important for the concept of the proof to show numerical sequences corresponding to the family. Namely, every point doubles, and adds 1 line, and every line doubles and adds 1 plane. This time, the four lines act as ‘walls’ to the current dimension of 2, surrounding a small amount of ‘plane’. |
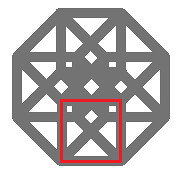 |
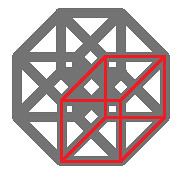 |
Again, we take our figure, the square, and drag it 90 degrees to itself. Now in our Three dimensional life, there is only two directions to drag it, either up, or down. This also made an appearance last time, on the computer screen, the only way to drag the line perpendicular to itself in the plane that was the computer screen, was either up, towards the top of the screen, or down, towards the bottom. However, we could just have pulled it towards us instead of staying on the computer screen. We wanted to make a 2 dimensional object so that all lines were perpendicular to each other when represented in the 2nd dimension in the frame of reference of the screen. Likewise, when making a cube from a square, in our world, there’s only two ways of doing it so that the lines are perpendicular to eachother in the frame of reference of our current three dimensions. Keep that in mind when we get to the next object. For now we contemplate the cube. Ok, when representing it on the second dimension, we draw the angle at 45 degrees, in the hope that the viewer will understand what it’s really representing is a line that is perpendicular to the two others. Understanding this is fundamental, please comment if this isn’t clear, or if you can’t see the red cube. In this case, we started out with four points, four lines, and one plane. Each of the four points followed their algorithm, of doubling and creating a line. Each of the lines followed suit, of doubling and creating a plane, and likewise the plane decided to join in, and doubled and created a space. The theme here, is for each part, it doubles and creates something one dimension higher than itself. This is the essense of the aforementioned proof of the numerical sequence. |
| Like always, we take our object, drag it perpendicular to itself (this time into the fourth dimension), and end up with this image. This image is the two dimensional representation of the tesseract. The two diagonal lines off of the starting point are meant to not be in the same plane as the vertical and horizontal line. The 8 points of the cube were dragged, duplicated, and created lines. Likewise up the dimensional ladder, as it were. Up until the space was dragged, duplicated, and created a hyperspace. Similarly, this can be taken further into a so called hypertesseract and beyond. I’d like to talk a little more about the tesseract, and it’s construction. For that I’ll go back to something familiar to most. |
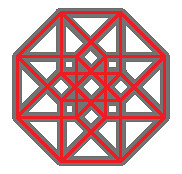 |
 |
What we have here is what I like to call an unfolded cube. Elementery schools tend to give kids a piece of paper, have them cut this design out, and fold it into a cube and tape the edges. The design here is four ‘blocks’ stacked one on top of the other, and the second ‘block’ from the top is completely surrounded by ‘blocks’. I’m using the term blocks in this way, because looking at the next picture will lead to the exact same statement. |
| This has four ‘blocks’ stacked on top of each other, and the second ‘block’ from the top is completely surrounded by ‘blocks’. See, didn’t I say the exact same? Well what is this? It’s an unfolded tesseract. In the same way kids fold up a piece of paper that started 2 dimensional, and folded it into the third dimension, the same can be done with this third dimensional object, folding it up into the fourth dimension and creating the tesseract seen before. If this is hard to see, think about how the paper was folded into the cube, and do a similar thing to this object. Faces that share the same line are the same face. Kind of like in the paper cube, lines that share the same point are the same line. Likewise stacking four tesseracts on top of eachother, and then having the second from the top be completely surrounded, spaces that share the same face would be the same space in the corresponding hypertesseract. [Aside: I have made some beautiful drawings back in the states, that match up every point, line, face, and space between this figure and a tesseract. It is essentially the same. If anyone would like to see or have a copy of this, just contact me and I’ll draw it up either on paper or computer depending on the request. I’d be more than happy to do that for anyone who’d like to see the matchups.] |
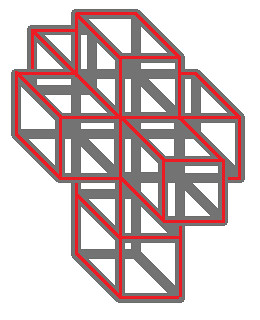 |
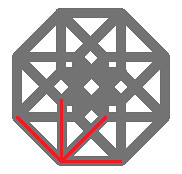 |
I want to point one more thing out. This image is all the lines connected to the starting point. Note as we traveled up through the dimensions, the number of lines connected to each point goes up accordingly. 0 dimension had 0 lines per point, 1 dimension had 1 line per point, etc. One more point, notice that to create a tesseract, start with the ‘origin’ point, and use each line exactly once in every possible order. I’ll explain by words with the square. Starting at the lower left corner, there’s two ways to go, either right, or up. Once a direction has been decided, theres only one possible line left to use, so in total there’s only 2 paths from the ‘origin’ point to the endpoint. The cube has 6 such paths, and tesseract has 24 such paths. Thus with these two bits of knowledge, it is easy to construct an nth dimensional object in this family, by taking a point, and n lines, and finding all orderings of the n lines. As it turns out, to find a nice symmetric 2d representations, the square’s outline is, of course, a square. The cube’s outline is a hexagon, and the tesseracts outline is an octagon. Similarly, the hypertesseract’s outline is a decagon. Notice that an nth dimensional family member’s outline would be 2n-gon. Also, drawing the 2n-gon gives n line segments that are at different angles. Thus a great tool to the beginning of drawing an nth dimensional member of this family. |
| I’d like to talk about naming schemes now. Especially with those last few lines, it’s easy to see why a naming scheme should be found. For this family I would like to put forth the naming scheme Perpingon. Thus a Perpingon(2) or 2d Perpingon would be the square, Perpingon(4) would be the tesseract, etc. Here are my reasons. First off I use a shortened version of Perpendicular-polygon, which is how this family is constructed by previous family members. I also chose polygon instead of polyhedra or other forms because it seems that the 2nd dimension is where most of the variety will begin. Almost all families will have a point, and line in the 0 and 1 dimension slot, and it’s only in the 2 dimension slot that families start to differ. [Aside: I say mostly all, because the family that includes nothing but a point would, of course, have a point and a point as the first two in the family instead of a point and a line.] Using this scheme describes how to build a member from a previous member, and shows where the pattern can be guarenteed to continue. For example my second introduced family will be triangles, tetrahedron (4 sided polyhedron) and hypertetrahedron can be said that the pattern is set by the triangle stage. However if a family were brought up that started point, line, triangle, icosahedron (20 sided polyhedron), and then after that the pattern is set, a naming scheme ending in -hedron could be used. Another consideration I had was to use the name of the numerical sequence associated with the family. That is why I’ll call the next family Pascalgon, for reasons to be discussed later. However that naming scheme is hard to use at an early stage, for sometimes the sequence is unknown, or unnamed. The Perpingon family’s numerical sequence seem to be the Square of the Pascal Matrix, and thus doesn’t have it’s own distinct name. |
| Here we are at the second family I’d like to introduce, the Pascalgon family. Again, the Pascalgon(0) (the 0 dimensional Pascalgon) is a point. |
 |
 |
Moving right along, we introduce a line. I feel this is a good time to discuss how the Pascalgons are generated. Know the saying, “Two distinct points determine a line, Three distinct non-linear points determine a plane”? Well, through any two distinct points, there is exactly one line that passes through both of them, and it’s guarenteed to be there. Less points, and theres an infinite amount of lines that can pass through, and more points voids the guarentee. Similarly with three points and planes. This works for all dimensions. For any n points that don’t exist in the same n-2 dimension, and no n-1 points exist in the same n-3 dimension, …, and no two points exist in the same 0th dimension, then there is exactly one n-1 dimensional space that passes through all n points, and it’s guarenteed to be there. The idea behind the Pascalgons is to be the smallest possible nth dimensional object in the nth dimension. A triangle is the smallest polygon, the tetrahedron is the smallest polyhedra. Notice that a triangle is 3 distinct non-linear points, and a tetrahedron is 4 distinct non-linear non-planer points. There’s the idea, let’s explore. |
| Here is our triangle. As we’ve already said, there are 3 points in the smallest polygon that determines a plane. Also, the triangle may not appear to be equilateral, but pretend it is, and it’s on a slant. That kind of imagination will help as we progress. Of course they don’t have to be equilateral, but then problems with angles and points matching up get in the way. Nice regular Pascalgons, that’s what we are looking for! |
 |
 |
Here we see a tetrahedron. Imagining it might be a bit hard, especially for non-gamers out there. There are four points, six lines and four planes in the form of triangles, and they make up one space. A better visual of this is the first figure here. [Aside: Interest in polyhedra could likely be satisfied with a decent horde of dice.] Notice on this one, that the outline can be made into a square with all corners connected. |
| Finally we have our 4d Pascalgon. 5 points, 10 lines, 10 planes, 5 spaces, and one hyperspace. Again we notice that it consists of n points (in an n-1 dimension), with all of them connected to all others. This makes sense, because if two points did not connect, one of them could be removed and still preserve the uniqueness of the dimension in consideration. For example, a square can be thought of as two triangles, with at least two of the corners not connected. Thus one of those corners could be discarded, and the other triangle still remains intact, thus the determined plane. Another thought here, just as a cube can be made out of folding paper, so can a tetrahedron. This time the design is in the shape of a central equilateral triangle, and each side is shared with another equilateral triangle, and thus four. these fold up so the outside points all match up at the top. Likewise, the tetrahedron can be combined with four other tetrahedrons, each sharing a face with the original, and then can be folded up with the outside points coming to one point, and thus the Pascalgon(4). I refrained from attempting to draw 5 tetrahedra in an unformed Pascalgon(4), due to not enough drawing skill to pull it off. If five 4-sided dice can be found, try matching them up and see what it would look like unfolded. |
 |
I’ve demonstrated two different dimensional families. I’d like to get on to the numerical sequences associated with these.
| Name of Object |
# Points |
# Lines |
# Planes |
# Spaces |
# Hyperspaces |
# Dimension(5) Areas |
| Pascalgon(0) |
1 |
0 |
0 |
0 |
0 |
0 |
| Pascalgon(1) |
2 |
1 |
0 |
0 |
0 |
0 |
| Pascalgon(2) |
3 |
3 |
1 |
0 |
0 |
0 |
| Pascalgon(3) |
4 |
6 |
4 |
1 |
0 |
0 |
| Pascalgon(4) |
5 |
10 |
10 |
5 |
1 |
0 |
| Pascalgon(5) |
6 |
15 |
20 |
15 |
6 |
1 |
| Blank Line |
= |
= |
= |
= |
= |
= |
| Perpingon(0) |
1 |
0 |
0 |
0 |
0 |
0 |
| Perpingon(1) |
2 |
1 |
0 |
0 |
0 |
0 |
| Perpingon(2) |
4 |
4 |
1 |
0 |
0 |
0 |
| Perpingon(3) |
8 |
12 |
6 |
1 |
0 |
0 |
| Perpingon(4) |
16 |
32 |
24 |
8 |
1 |
0 |
| Perpingon(5) |
32 |
80 |
80 |
40 |
10 |
1 |
Ok, we have the data, lets look at it. Well the Pascalgon data seems remarkably close to the Pascal Triangle… Pascalgon, Pascal Triangle… coincidence? I think not. For those who aren’t familiar with the Pascal Triangle, in laymans terms, to find an entry you add the entry directly above it, in the table, to the one to the upper left of the cell you are trying to figure out. In more mathematical terms this is (n|m) = (n-1|m) + (n-1|m-1), where (n|m) means ‘n choose m’. Now looking at the Perpingon Family, can anyone determine what the pattern is? The answer is (n|m) = 2*(n-1|m) + (n-1|m-1). Ok, this basically means double the number above it and add it to the number to the upper left. But does that make sense? Yes.
Convincing of the sequence: Remember how we created a square? We took the line and two points, doubled them, and created a plane and two lines. So lets pretend we want to figure out the number of lines in a square. Well by the formula it means we are going to have twice the lines as the Perpingon(1), and also an extra amount of lines equal to the number of points in the Perpingon(1). Ok, the first part is the fact that when going up a dimension, the object doubles, and creates a new object of a higher dimension. So a line will double, meaning twice as many lines as the previous, but also for every point, they are going to create a line.
As for the Pascalgons, the formula states, that the number of lines in the new Pascalgon will equal the sum of the number of lines in the old Pascalgon plus the number of points in the old Pascalgon. The first part means that no lines are lost when going up a direction, the second part means that when the new point is added, it is connected to each of the other n points, making n new lines. To get a visual of this, look at the progression from the Pascalgon(3) to the Pascalgon(4). In the Pascalgon(3), there are 6 lines. In the Pascalgon(5) those six lines are still there, plus with the new point added, it connects to the four other points, creating four more lines. 6 lines in prev, plus 4 points in prev equals ten. So go ahead and count the number of lines in the Pascalgon(4), and if you don’t get ten, count again.
Where to go from here?
That depends on your level. Someone completely new to these concepts, and higher math should start by pondering on these ideas, and let the idea of higher dimensional objects become familiar. The next stage would be writing up some actual formal proofs proving the sequences will hold for the whole family. After that, I’ve added some of my own thoughts and theory into it, so think about my naming schemes, and options of such. Beyond that lays a slightly more dangerous and exciting road. That road is the road down exploring other Dimensional Families. Determine how a new family member will be built on the previous, and whether there is any ‘dangling’ lines or such. Those just starting on this route, I’d suggest thinking of the Pentagon/Dodecahedron family. My hint would be start with a pentagon, surround it by other pentagons, and then double that to be able to make the Dodecahedron, would the next step be surround that by Dodecahedra and double it? What would the pattern be? What naming schema would be associated with it? For those who want to stay on that path, go on to hexagons and heptagons. Others might want to consider really complex things like Dimensional Families whose members contain concave segments. Again, what would the numerical sequence and naming be like? For those out for a real challenge, pick any triangle sequence (Like the pascals triangle or it’s square, both demonstrated here) and attempt to figure out what the corresponding Dimensional Family would be like, or prove that no Dimensional Family can correspond to the triangle.
Please read:
There are a few issues I want to discuss. First of all, all images contained within this post have been made completely by me with the help of Photoshop. As such, I express complete permission to use these images in any way you like, including for profit, with or without attributing me. These are completely free images. Secondly, if you’d like the Photoshop files, which includes layers for each line in the background and foreground, they can be found here for the Pascalgon and Perpingon. Thirdly, if you’d like any additional material along this line, including higher resolution versions, or the unfolded images with point mappings, contact me and I’ll be happy to make them for you. Fourthly I would deeply appreciate that if you come to any bit of further understanding, besides what’s written in this post, about these topics, please contact me and let me know what it is that you discovered, or worked on. Especially if you take my hints on the “Where to go from here” section and write proofs or explore further, I’d love to be included and allowed to expand my own understanding. Fifthly, Thank you all for reading this, and hopefully enjoying it. Please let me know how you liked it and if there’s anything else you’d like me to go into. Travelling dimensions takes both abstract, artistic views as well as logical, theoretical views, and I hope that everyone can enjoy this topic, whether it’s working purely with numbers, or drawing what a 2×2x2×2 block of tesseracts would look like. Thank you all very much!
3 Comments
In a word, awesome.
(0:12, 0.2MB)
Interview with Steve Mendoza on our shared field trip to Okinawa from the Friends World College East Asia Center.
This is my first podcast in life. I was mainly inspired by Ayme Frye who has been working with Aaron and generally getting the whole Podcast thing. Also, I learned that my iBulldog, made by MPIO who doesn’t seem to want to acknowledge that they made it, could record as well as play, and as I was trying to figure it out, I noticed Steve just sitting there minding his own business. The rest is, as they say, history.
Also, Since I’m here, I’d like to point out I added a Podcast category, which of course has it’s own feed.
4 Comments
Herring Sandwich
I would like to point out that I just got a hit referred from google from the search of “Herring Sandwich.”
Everybody grows in their blogging life, and I’m just proud that I’ve finally made it to my Herring Sandwich hit. I promise to keep working hard, so that one day I can achieve my goal of Letter Q in the Privet Bush.
2 Comments
Surprising Truth
Hardly any Real number is divisible by 1.
4 Comments
New Category
Well, I added a new category named ‘Site Maintenance’ in which I’ll post things like this post.
Besides that I have three things to put out there.
First, I added a Quote Plugin from Zombie Robot which is really good. This plugin is for Word Press only, I believe. Unlike other quote plugins, this one was made for the purpose of the user managing the quotes. Some quote plugins I’ve seen, all the quotes are hard coded into the plugin, thus if the user wanted to add or remove one, they’d have to mess with the code. ZR’s plugin, however, has a really easy to use interface. Once downloaded, and unzipped, one file is sent to wp-content/plugins and the other goes to wp-admin. After that, going into the Plugins menu of WP, activating wp-quotes gets a sub menu to appear under Manage. This new sub-menu, named ‘Quotes’ for some reason, provides a user friendly way of adding quotes with their authors, and visibility.
As you should be able to see on my site to the —>, I have added a bunch of Douglas Adams’ quotes. All the quotes I have up there are those that I could find online. Once I get back to America, I shall be going through all of Douglas Adams’ books and adding a bunch more!
One thing I plan on asking Zombie Robot, and possibly doing myself, is to set categories for my quotes, so that I can have two sets of quotes on the page. This would also be usefull to people like me who are foolish and have two distinct and major topics to their blogs. Such that I could have a Martial Artsy quote for those viewing that set of categories, and a Sciency quote for those viewing my Tech Category.
My second point of discussion today, is that between Thursday, March 2nd, and Monday, the 6th, I shall be attending a Field Trip to Okinawa. This is for a class on Japanese Minorities, and it shall be vastly interesting to see the interactions between the Okinawans, the Japanese, and the American Soldiers. I’ll also be visiting one of the bases, so that will be awesome, as they used to say in my generation. I’ll be taking pictures, and hopefully update my Japan-Webjournal each night, so if you are interested, check it out!
My third point is that I added a FAQ page! (I set the page up to allow comments, but when I go there no place to leave a comment appears… this could be because I am me, and thus shouldn’t be leaving comments on my own pages. If someone could comment on this post letting me know if a comment box appears or not on the FAQ page I’d be appreciative!)
-Chobbit
4 Comments
Zenless Arts?
In my bloglines account, this little gem popped up from Michael Riehle’s blog: a post about religion and Aikido.
I left a dojo years ago partly because of the emphasis they placed on Zen training. A lot of people argue about whether Zen is religion, but Zen is rooted in Buddhism and Buddhism is religion even if it isn’t in the same vain as some other religions. It isn’t that I have a problem with Zen, but I don’t subscribe to it and it isn’t what Aikido is about to me.
This topic is something I believe is a very big point in Martial Arts practiced outside of Japan. The first thing I’d like to put forth on this topic is how Japanese view religion in their lives. Rather, how they believe themselves unreligious. Religions in Japan tend to get merged into society, integrated with every other religion from before. For the Japanese themselves, they don’t see Martial Arts as being religious. The question is, is this the truth?
I’ve read and heard of many cases of Westerners being ‘interested in Zen’ and thus the reason for coming to Japan. The most moving case for me is from the book Armed martial arts of Japan : swordsmanship and archery
Following that link provides a good review of the book, and most interesting here is:
He also considers Western misperceptions of Japanese traditional martial arts and argues that, contrary to common views in the West, Zen Buddhism is associated with the martial arts in only a limited way.
I was particulary interested in Kyudo at the time of reading that book, and I’m thousands of miles away from looking at it, so the following may seem a little fuzzy for that reason. If I happen to find a copy in the future I’ll come back and add a comment to more accurately present the following.
In the book, Hurst confides in us the history of Kyudo as far as he and his research could tell. A student from England was interested in Zen, and made contacts in Japan and ended up becoming a student of the man responsible for compiling Kyudo. During his stay, his obsession with Zen became apparent in his writings about Kyudo. Hurst mentions a case that may or may not have actually happened, but the story goes that the student asked the master why he wasn’t allowed to aim at the target, and unsatisfied with verbal answers, the master lit a piece of incense, and placed it under the target, then proceeded to turn off all lights so the range was pitch black. The master then proceeded to do the form, and let loose an arrow. The sound of it hitting the target echoed as the Master calmly continued to the second and last arrow. After letting it go, the sound of arrow hitting arrow echoed out. The student asked how he could do that, and the only answer he could get through the translator was “It aimed, not I.” The student then took this and assumed a Zen association.
Anyone who’s studied Japanese understands that quite often the subject of the sentence is left out. In this case whether the ‘it’ the master meant was some sort of zen spirit, or the idea of a perfect form, we shall never know. However, the student applied a heavy Zen-oriented view on it, and through out his life in his writings, whenever he’d mention the incident, more and more Zen qualities appeared in it, even to the point of vastly changing what the master said to better suit his view.
Undoubtedly, many concepts deemed mundane in classical Japan can be viewed in a religious light by westerners. However, is this any difference from Egyptions worshiping cats… Would the cats have not existed if the Egyptian religion wasn’t around? That’s how I personally view Zen (the religion) and Martial Arts (the cats).
Another blogger with a similar Idea is the Atheist RA, who posted a post entitled Tai Chi Chuan and Atheism. The post includes the following paragraph:
The reason for that response alone is based on a number of misconceptions. Tai Chi (herein referred to as TCC) is based primarily on Taoist philosophy (Taoism in it’s purer form was emphatically not a religion). TCC is based on Eastern concepts, such as ‘Chi’, ‘Shen’, ‘Jing’, and such. We all have Hollyweird to blame, in re: the ridiculous stereotypes accorded to any martial art whatsoever. It’s this marketing ploy, this effort to drape any and all MA(martial arts) in mystical crap of some sort, to bring in a few extra bucks.
He points out that the main thing attacked by Westerners who attempt to pin religion to Martial Arts is Chi. He goes on to state what many Martial Art practitioners believe, in that Chi is nothing more than the energy that flows through your body. In basic physics, for any movement to occur, an amount of energy must be expended. As blood flows throught the body, and in fact every cell has internal movement, there must, by logical consequence, exist energy in the body. This is Chi. Whether the idea of ‘mastering’ chi and gaining control of surroundings is possible or not is currently something for religion. However most Martial Arts don’t deal with Chi in this mystical sense, but rather in the sense of internal energy. It is my belief that ‘Chi’ isn’t a magical force, but the energy that exists within us allowing us to move, breath, and live.
If this is taken care of, what else is there for the Westerners who insist on applying a religion template onto Martial Arts to attack?
3 Comments
Copyrights
The copyright issue had me leaning back and forth quite a bit in the past. Mostly on my programs, and such like that. I think it’s basic human nature to ‘want’ to be able to be traced back to. Look at the ‘need’ for children to ‘carry on the name.’ Accreditation is a desire to ‘continue living.’
While it’s easy to say that if one person writes a very good book, and someone else copies it and makes a few minor changes and provides it to everyone, that it is bad in every sense of the word. However, what about recipes? If a cook creates a recipe, and another cook samples it, and creates the same thing for their own kitchen… what is the common view?
There is a case in Europe to allow recipe’s to be copyrighted. And while this guy isn’t looking for money, only accreditation, it could soon lead to very ‘preposterous’ cases.
This case has brought me straight to the ’sharing’ side of the copyright issues within milliseconds. While one could say, “A recipe is nothing more than the ingredients and cooking,” the same could be said with, “A painting is nothing more than the paint and the strokes.” Everything that has been copyrighted to date can be expressed back into terms of a recipe, and for some reason, copyrighting a recipe seems so over the top absurd to me, that now every other copyright issue comes across the same way.
Why create? Why go through the process of taking ‘ingredients’ and putting them through a ‘process’ to make an ‘object’ if not to share it with someone else? Economics is all about this; Supply and Demand. If there’s a demand for something, it should be supplied, and if something is supplied, there’s probably a small demand for it. This is what marketability is, creating a demand for a product. Everything in this society is about creating something for someone else. However, I believe the one flaw to this society is the reasons behind the creating, and that’s an immediate gain of ‘wealth.’
It’s been said many times and many ways, Merry Chri… wait, that’s not where I was going. I was going for: “A society is built on the contradictions of the previous society.” There is already a huge movement for ’shared products’ out there. Look at the GNU license, it’s a ‘copyleft’ of the guarentee to be able to use and share. Also, I just added to my blog a Creative Commons button. Creative Commons is an alternative to the automatic full copyright, without giving full permissions. In fact, many varients are offered depending on what the preffered protection is desired. I believe the most common is the ‘non-commercial share-alike attribution’ in which the product can not be used to make money, however besides that it’s free to share and use in any way desired, and it’s prefered that the resultant is shared under a similar sharable scheme and that accreditation is added.
Looking at this, the idea is to encourage others to share. However two points must be added due to our current culture. Non-commercial is clearly a resultant need to step away from the current culture, and accreditation is that basic need to be ’seen’ that I discussed at the beginning of this post.
I believe the hardest part for individuals moving from the old commercial society to this new ‘idea’ is the ability to ‘give up’ what is ‘theirs’ and allow it to be mutated and evolved into something more. P2P-kids are used to ‘getting other’s works’ however it’s still a challenge, even for them, to give up what society has taught them is ‘theirs’. I would like to offer this one point. If you think something is ‘yours,’ relate it to the guy wanting his recipe’s copyrighted.
3 Comments
Board Clearing
This is another problem from my puzzle solver section. In a hurry to solve this one, I had used the brute force method and hard coded method. Unfortunately after not too long, the puzzle started changing, and my hard codedness failed. I had then removed the hard codedness, and now I’m focussing on removing the brute force algorithm.
The Problem: This is a classic. The board is a 4×4 grid, filled with either 0’s or 1’s, and you have a set stack of tetris-like blocks that change 0’s to 1’s and vice versa. The goal is to rid the board of 1’s and leave it completely homogeneos. A version of this game that was marketed is ‘Lights Out’ In which there is a 6×6 grid with lights that are either ‘off’ or ‘on’ (0 or 1), and when you select a grid point, it, and it’s four neighbors are switched, (one piece that is a 5 block cross). The goal, obviously, was to get all the lights out.
Solution 1: Brute Force
In this solution, the idea is to place the first peice on the board in the first position it was allowed, and then place the next peice, and repeat until the last peice. After the last piece is placed, check condition. If it’s not a solution, then increment where the last piece is, and check again. Once a piece has incremented through it’s entirety, increment the piece before it, and try again.
Good points: Exhaustive, if chosen, this method will find all possible solutions.
Downfalls: Time consuming, and space consuming.
Where to next?
Well, I’m assuming that nothing is hard coded, and thus the board size, and the number, variety, and shapes of the pieces are provided by the user. Also the board layout, and the base of the puzzle (ie 0-1-0, or 0-1-2-0, or more complex 0-1-2-1-0), and the number of changes of each ‘block’ in each peice is also provided.
Next solution? I wonder if it would be better if the program looked at the pieces first, and ordered them, and determine if there are a bunch that could cancel eachother out. For example, you could solve a 3×3 with the only ‘on’ light being the center, if you have 15 1×1 blocks that toggle the light. Of course you turn it ‘off’ with 1 of the 15, and then the other 14 you double toggle a light somewhere on the grid. Thus three types of solutions exhist;
- All blocks are used, and it’s a solution
- Solution is found without using all blocks
- A Solution exists with all blocks used, but also with less blocks used.
The capability of the Brute force method mentioned above is best suited for only #1. However, if a ‘completed’ check was added after each block was moved or placed, then the other two would come. However, there’s probably a way to do it without a brute force method.
Comments
AI vs Rich Diamond
Rich Diamond is a tile based puzzle game. The objective is to collect diamonds, and reach the endpoint. However many dangers lie in Rich’s way, and many puzzles. Core Concepts has a daily puzzle section which often features a small Rich Diamond puzzle. These are 10×10 (I might be a few squares off) puzzle grids.
In this post and the ones that follow, tracking back, will be about methods of creating a program that would be able to first, solve the small daily puzzles in the least moves, and then to solve the regular levels with the maximum points.
Solution 1: Brainless
I name this brainless, because that’s what it is. In fact, I wouldn’t be surprised if some easily programmed AI could come up with this. What is it you ask? Well you’ll be sorry to hear, it’s the ‘try all possibilities’ method. First move, take Rich north, check puzzle solved. Then take him north again and check. Repeat for some number of moves, (In the small game, a ‘guarenteed least number of moves’ is available, so use that as a sentinal to check if Rich has moved more than this number.) Once the max number of moves is reached, go back one step, and try going east instead. Then north until max is reached, then go back and try south, ~, west, ~, go back one step further and try the next one there ~. If a finish path is found, store the path and number of moves if it is less than all previous solutions.
This solution is obviously quite exhaustive, infact it’s guarenteed to find the shortest path for rich to take to finish the puzzle, as long as it’s possible with less than N moves, with N being specified.
The downfall? Many! First off, this takes quite a bit of memory (especially once we move to real puzzles), and time. Despite the speed of computers, I wouldn’t doubt in most cases a human could sit down and look for a bit, and solve the puzzle before the computer was half way done trying. Another problem is that the puzzle needs to be restarted everytime path movements change. This is needed, because if Rich walks near a boulder and then walks away, the puzzle changes, so going back a step won’t really get you to a previous state.
That second problem can be helped, by saving the state before making a move, then reverting when needed. This of course is asking for loads of memory however.
The real question isn’t about how to make this method less intensive, but rather to find a better method.
((Ps, comments or suggestions are more than welcome!))
Comments
Path finding through warps.
It is pretty clear that given a grid with ‘walkable’ and ‘unwalkable’ nodes and a static start and end point, using A* is the best pathfinding algorithm. Besides ideal conditions, many other topics have come up, as evidenced by this great article by Bjorn Reese. However, one topic that seems to me almost taboo is ‘warp portals.’ One of the more common ’solutions’ I see to this, is to use Dijkstra’s Algorithm to determine a path to the finish point while possibly utilizing the warp point. However, I think that there is a lack of understanding the problem here. The real question, when dealing with warps, is are they known about or not. If they are viewed as part of the ‘terrain’, then Dijkstra’s Algorithm would be necessary to find them, and A* would find the shortest path to the finish point without touching warps. However, if it is known that these warps exist (even if where they turn out isn’t known) it would only require a few additional ‘threads’ of A*, which would save time.
In what cases can we assume that the warps are known about, and that they aren’t? I believe that in all realism, if the exact location of the ‘finish’ point is known, then there’s a good chance that the location of the various warps would be known too. On the flipside, if the finish point’s where abouts aren’t known, then an algorithm like Dijkstra’s will be used anyways, saving us the trouble of worrying about it!
Comments
Separated RSS Feeds
Small post to let everyone know that I have travelled the perillous journey through code (1 click, and 1 copy/paste) to provide my viewers with a way to see what they want, without the other junk!
While all of these categories are my interests, not everyone is me! Therefore, if you find my Tech section more interesting, then you can subscribe to just that, or if you are only interested about Shodo, well you can subscribe to only that if you so choose!
To this, I must say: Let the fun commence!
2 Comments
What’s too strict?
Responding to a conversation on my post about keeping focussed every moment, AikiThoughts blogged about thinking through this idea, and came up with a barebones schedule and ended with this:
This is just a bare-bones, on-the-fly example. But you notice a common theme? Moderation, focus, a clear delineation, but not separation, of work and family life. It doesn’t seem that complicated, yet how many of us live life like this? What would happen if we did? Would our lives have more focus? More enjoyment? This certainly isn’t a hedonistic lifestyle. Yet I can’t help but wonder if our lives wouldn’t be better if we lived with this sort of simple focus and dedication.
This idea was also expressed by Aaron in his comment to my post:
I like this post, Paul. The idea of being fully aware, while being modest and focused throughout each moment of the day is the end in and of itself. Being one with the process of life is both the goal and the means in one.
I, however, think I have a small problem with this! Of course it depends on the type of lifestyle that’s wanted, but keeping focussed and constantly training doesn’t necessarily equal having a completely prompt and modest lifestyle. I feel that having a clear mind, and constantly training shouldn’t surpress all emotions, but in fact play on them.
In a lot of fantasy, there are almost always two distinct races, be it Elves and Dwarves, or Vulcans and Klingons, or a myriad of others. These seem to be based on a ‘emotionless intellect’ and ‘passionate animal’ ideas. In these places, Humans tend to be a mixture of both, a midpoint. While no one could argue the strength of Dwarves or Klingons, or the intelligence of Elves or Vulcans (well…unless you are a Dwarf or Klingon!), any story always had the third race, Humans in most cases, pull through because of their ability to go either way and combine as necessary.
If you understand where I was going with that, then congratulations, but let me explain anyways. Being in Japan, and especially taking Dr. Houser’s Course, has led me to see how much emphasis is placed on correct form. If taken too far, this leads to empty copying of forms. To keep the forms’ meanings, awareness that everything is up for change until the time passes is necessary. Getting up at the same time, and doing the same things at the same times, every day, get’s pretty monotonous, and that in itself can lead to a wandering mind. I believe that a completely scheduled lifestyle (the Elf) is just as bad as a completely random lifestyle (the Dwarf). The ability to keep focus through out the tides of life is the true mark of training.
2 Comments
New Links
I’ve been searching recently for some good bloggers to fill out my interests, as this blog seems to be in a martial-arts oriented mood.
Using Feedster, I searched for “programming theory” and got two really interesting finds.
I’d first like to introduce Derrick Coetzee. His posts are mainly descriptive about various topics that, as his Blog’s title suggests, are development for developers. His work is well packed, and quite understandable, even for beginner developers. For example, I’d like to quote his Unrolled Linked Lists post:
Today I’ll be discussing unrolled linked lists, a simple variant of the linked list which has many of its desirable properties but exploits the cache to yield considerably better performance on modern PCs.
Viewing this post, he uses a lot of good techniques to help him. Using links, diagrams, and psuedo-code, he enforces his structure of introduction-explanation of ‘problem’-solution. As I’ve stated earlier, his posts are also ‘understandable’ even for the novice programmer.
The second blogger I’d like to introduce is Iggy Chaos, who I also found through that Feedster search, linking me to this post, which talks about why ‘kick-ass programmers’ can’t find jobs. However what got me hooked was his Squirt Gun Offense post, which I’ll share an excerpt (but the whole post is more than worth reading):
Shooting someone with a squirt-gun is probably illegal (squirting with intent to dampen) but it’s not likely you’ll get busted for it. If you do it, you’ll probably make the target mad - but there really isn’t much they can do about without stepping over the invisible line themselves. If they whack you - its a whole new ball game. The judge is not going deem assault “ok if first squirted with water”. A better plan by the hotel manager from our first story would have been to simply walk up to the business man and start pelting him with shots from a super soaker. What’s the business guy going to do? Tell the cops they squirted him? Heck, he stole donuts - I think its even.
Iggy Chaos has a well developed sense of humor that makes his posts gems. For example, I’ll add another excerpt from his Mom, I think I’m a Cyborg post:
Now similarly, I might ask “Do you know what time it is?”. And, at the very instant of me asking, you may not. However, the common response is to raise your wrist to your face and say “Yeah, its 4:30″.
You liar. YOU did not know. Your watch knew but took credit for its perpetual temporal omniscience. I always know what time it is cuz dadburnit - I have a watch! In effect, we have extended our concept of self to include our watches - thus in Dr. Clark’s claim we are cyborg.
While computational theory doesn’t play a named role with Iggy, I would still recommend adding him to the watch list.
Comments
Paired Ki Excercises
In Aikido we have a paired ki exercise which both practitioners are in right hamni and right wrists back to back with eachother. Then you either push or accept and deflect depending on the opponents ki.
A few notes I’d like to share: Use your one point, all motion should come from the hips. Also, keep your wrist directly infront of you… think tenkan where your wrist stays infront of your one point as you turn… Same idea. Also, obviously don’t push to hard, otherwise you fall!
Comments
Keeping Focus
On a comment to my previous post, James Doolittle had pointed out something which I feel is a common feeling amoung younger practitioners:
The Bushido Shoshinshu was written as an expression of elder samurai and their disdain for the youth at the time. During the period of peace, these elder samurai felt the younger generation was losing the martial aspect of their knighthood. So, it seems that the generational laxity agrees with AikiThought’s observation, that the discipline of warriorship can only be attained during a time of battle. On the other hand, in another section of this book, Taira instructs that while being a master in these martial art forms is important, it isn’t necessary to begin training at a very young age in a time of peace. It seems like he is betraying the purpose with which he wrote this book to some degree; perhaps the reason samurai lack the miltary magesty of their ancestors lies in their integration of martial and fine arts. Maybe a samurai’s brain only has enough room for effective killing methods and stately character only! I believe the addition of caligraphy, sumie, and various other non-martial arts lead to them to their disassembly, and that the same is true today. We’re learning about history, writing, researching, and blogging while we try to learn martial arts–either out of a lack of training time because of these other things or a diversion in our ability to focus on martial arts alone, college students are not suited to become masters of martial arts.
My archery teacher, who is clearly a master in Archery but also practiced Kyudo, and Tai Chi, once said, that the mind doesn’t know the difference between imagination and reality. If you have a free moment in the day, use your mind to focus on a ‘target’ and imagine your body going through the steps of shooting, and you have just shot an arrow. While it doesn’t help your muscle memory, it continues to train your mind.
Taira says, “when off duty you do not simply lounge around; you read, practice calligraphy, contemplate ancient stories or ancient warrior codes.” Looking closely, all of those, especially in Japan, are about training the mind. Never let the mind stop training, or to lose focus.
James says that we have a lack of training time, or a a diversion in our focus. I believe that to be a master, that this is the wrong thinking. Even if a sword or bow isn’t handy, the whole day is a training period. Other aspects of life do not exist to divert attention, but rather focus it.
Believing all ‘real’ samurai trained from morning until night each day that there wasn’t a battle, all american soldiers do pushups from morning to night until there’s a battle should also be believable.
James uses the term ‘master’ in a dubious way. I think AikiThoughts has a good post on this. To me, Masterhood has 2 distinct meanings. I see the distinction between the Kyu ranks and the Don ranks as a distinction of student and master. I also see the term to ‘master’ something quite unachievable in martial arts. A goal to strive for, to keep you continuously training. I have many teachers that have achieved greatness in martial arts, such if there were an old-style war, I wouldn’t want to be against them. And they do it with full time jobs, or even while in school. It just takes the proper mental attitude towards training and life.
5 Comments
Jack of all Trades
AikiThoughts responded to my Multi-do post, and brought up an important point:
One other item I’d like to point out: in more traditional times, training for war was often a necessary and full-time occupation. Consequently, there was time to practice several different arts, because most of your day would be solely devoted to training. Now, martial arts training is a small slice of our daily lives. For many of us, it is difficult to carve out two or three hours a week for our training. Given that, training in multiple arts today requires someone who can make the time commitments necessary to give these arts at least a modicum of attention and focus. This can be extremely challenging… and while I applaud those who can do it, lack of time remains the another prime reason why I often caution people from practicing more than one art.
Self defense, after all, is not an activity where “jack of all trades, master of none” is sufficient.
Due to experience in a college setting, Every semester there would be one or two students trying to take as many martial arts as the school would allow. Unfortunately they hadn’t practiced any of them before hand. This means that they were trying to pick up the basics from 3-5 arts at the same time. Every single one of them ended up dropping out of martial arts all together.
When learning the basics of a martial art, it requires the most attention. Only once the basics are in muscle memory as AikiThoughts put it, can one even think about looking at other arts. But I want to warn against thinking that the basics are an endpoint. Too often I have heard of people who wanted to ‘pick up the basics from a bunch of martial arts, and then create their own.’ When questioned, they tend to mention Bruce Lee. However, their logic has a flaw.
The famous Yip Men taught Bruce his basic skills, but it was not long before he was mastering the master. Yip Men was acknowledged to be one of the greatest authorities on the subject of Wing Chun a branch of the Chinese Martial Arts. Bruce mastered this before progressing to his own style of Jeet Kune Do.
“Bruce mastered this before progressing to his own style.” Even though he was one of the rare geniuses of this world, he didn’t even attempt to learn multiple martial arts at the same point.
A Jack of all Trades doesn’t just apply to Jack of all Trades School, even in the olden days, the would have a strong foothold in one trade before situations had them move to the next, and even having moved on, they still practiced the other trades.
2 Comments
Aikiwiki
Turns out there’s a Aiki page dedicated to all styles of Aikido, and they also have their own Wiki!
If you are practicing Aikido, I say check out the site and see what you think and if you’d like to help contribute!
Comments
Aiki goals
From AikiThoughts:
George Ledyard, Cheif Instructor at Aikido Eastside, an Aikikai dojo, wrote this interesting article about training goals and deciding where one fits Aikido into one’s daily life.
I’m not sure how I feel about this article. One the one hand, I agree. You need to define your goals in your training, to determine where you want to go and how you want Aikido to fit into your life. Also, as Sensei Ledyard states, you need to be honest about how Aikido fits into your life, and not delude yourself into thinking your training one way when, in fact, you’re training another way. I have seen students that train diligently, yet refuse to acknowledge how important Aikido is to them, and I have seen students who train infrequently, yet claim to be passionate about the art. Both are ultimately unsuccessful mentalities. So in this aspect, I agree with the article.
What I have issue with is that the article gives me the impression that you must choose, and choose now, how Aikido is going to fit into your life.
I too agree with what Mr. Ledyard says, and what is mentioned by AikiThoughts.
I think there is a definite need to Choose your goals now. Do you train to become a head of a dojo, or do you train to be able to protect yourself in your job, or do you train to hang out with a group of people?
Knowing what you want to get out of Aikido will allow you to adopt the most appropriate training schedule. This is not, however, static. Everyone has their own lives, that will undoubtedly change the way you train. But everyone also has a natural change of feelings. If you are unsure about what you want out of Aikido, there’s a good chance that if you start going through some hard times, and your emotions aren’t in tip condition, then you might choose to ’stop Aikido for a while’ which turns into never practicing again. However if you set your goals now, “I want to be a head of a dojo, and help many others find their way,” then when hard times come, that will be something you can hold on to, and even if you don’t practice every day, or even every week, you will always have that goal to keep you coming back.
1 Comment
Milti-do
The following comes from the blogger: Way of the Bow
In the history of budo we have seen many examples of legendary teachers and practitioners who have not only studied more that one martial art but have excelled at pursuits that would seem to have a tenuous connection to the martial way.
He then goes on to ask a very important question:
How important is it for kyudoka to study other martial arts and learn other skills, and why?
From personal experience, I think this is a wonderful idea, and not just with martial arts. I currently practice Iaido, Kyudo, Shodo, and Aikido, but I also practice Archery as a sport.
There is certainly a set of Ideas to be gained from practicing Japanese martial arts. Mainly the focus of correct form, and correct mind. However, with Iaido, Kyudo, and Shodo, you don’t get the proper training in correct feeling. Even in Aikido, it is mainly about practicing the forms, and getting out of the way, and there’s only a small percentage of time spent on actual application. However when practicing archery, I have a teacher who also did Kyudo and Tai Chi in the past, and applies some of the thoughts to his teachings. So while his students are almost all ‘westerners’, they do get to experience the ‘form-based’ ideas from the martial arts. However, he also spends a lot of time having us in competitions, standing behind us, trying to ‘freak us out’, etc. This is to develop the correct feeling. In olden days Japan, the warriors would be facing real life (or death) situations. Modern Kyudo and Iaido don’t properly train you to not ‘freak out’ during your training. Granted War with bows and swords are unlikely in this day and age, but there are many situations which you will find yourself nervous, angry, depressed, or any number of other ‘unhealthy’ emotions.
While we can’t simulate real battle to get you nervous, certainly doing archery or another ‘competition’ sport in front of a huge audience with winning being the most important factor, and if you don’t have proper training in correct feeling, your shot is going to be off, and you will undoubtedly fail.
Another aspect of the question, is whether to practice alternate martial arts? This is a tricky and personal question. I currently practice 4, and will continue them for quite some time. I use the distinction of, Brush, Bow, Sword, or Empty. In this way I can react to situations depending on what I have with me.
To exemplify this, in the book Another Fine Myth by Robert Asprin, the Main Character (a Magicians Apprentice) asks a Demon why he can’t learn both physical and magical attacks and defenses. Aahz, the demon, throws a log at Skeeve, the apprentice, and tells him to block it. Skeeve first attempts to use his hands, but then decides he should impress Aahz by using magic, and ends up getting hit during his indecision.
That is a major reason why two arts that share the same utensils shouldn’t be mixed together. Like Aikido and Karate, unless you can be very skilled and train your body how to react to certain situations (and which art to react in), then they shouldn’t be mixed, otherwise you end up in indecision and losing the battle.
As for the benefits of training both Iaido and Kyudo? In the modern day, I don’t think one exists. In ancient Japan, both were necessary for war. However today, they’ve both been toned down to ’self development’ types of arts, and the only difference between them is the muscles they condition.
3 Comments
« Previous entries ·













